Ce défi optique défie votre perception visuelle
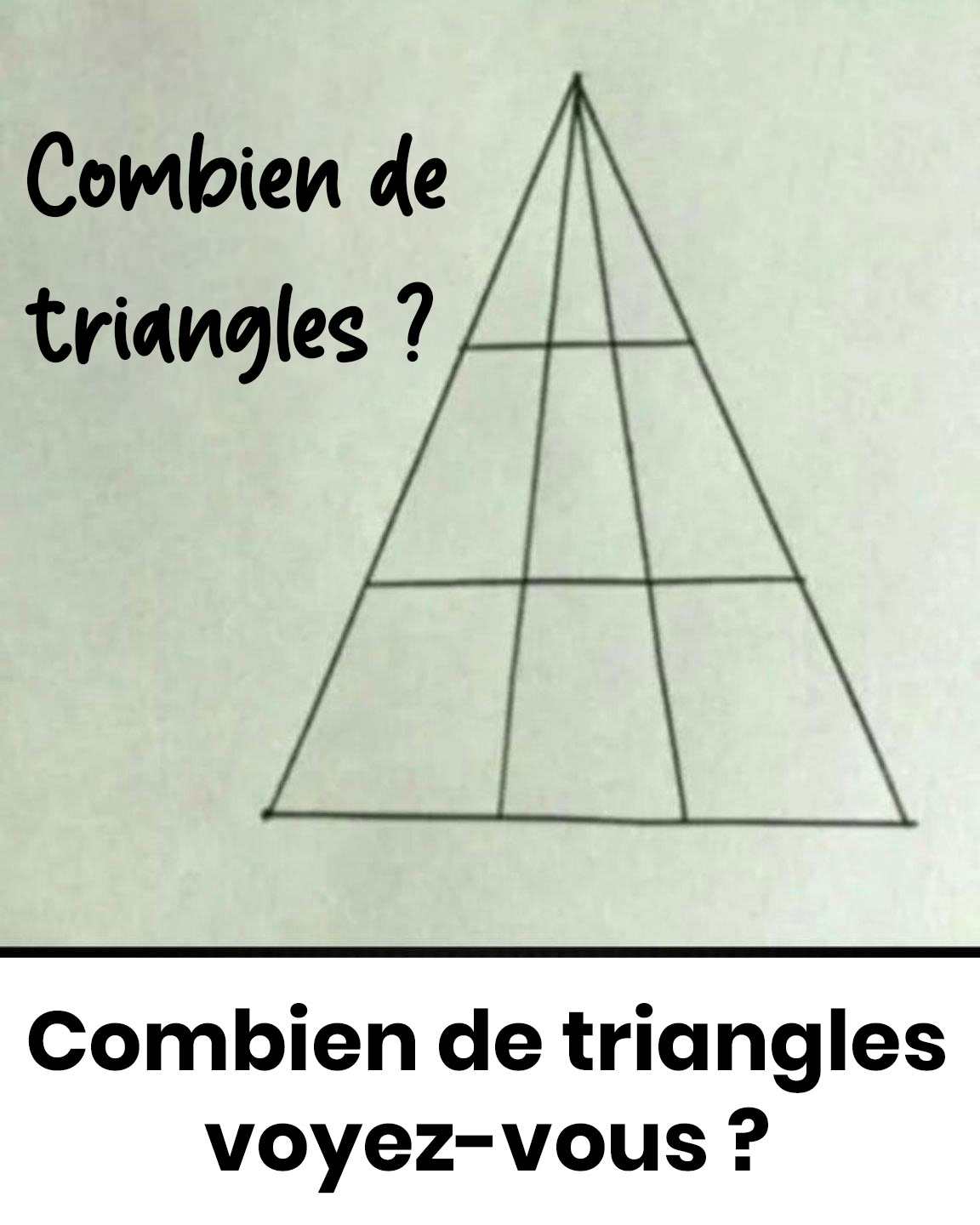
Cette énigme visuelle d'apparence basique contredit étrangement notre logique première. Sa composition géométrique recèle des subtilités que notre esprit peine à discerner immédiatement. Découvrez l'approche méthodique qui vous permettra de résoudre ce mystère et de surprendre votre cercle d'amis.
Le mystère des triangles cachés
Notre cerveau a une fâcheuse habitude de ne repérer que les triangles les plus évidents, en laissant de côté ceux qui se forment par la combinaison de plusieurs éléments. Résultat : on passe souvent à côté du nombre réel. Dans cette configuration bien connue où quatre étages sont dessinés par trois lignes parallèles au bord inférieur, la bonne réponse est bel et bien 27.
Si vous avez personnellement estimé autour de 26, vous avez probablement omis l’un des grands triangles composites – souvent celui qui s’étend sur trois niveaux, ou une version plus discrète sur un côté.
La méthode infaillible pour ne plus se tromper

Commencez par les triangles pointant vers le haut, en les classant par taille :
- Petits (1 niveau) : 10 unités
- Moyens (2 niveaux) : 6 unités
- Grands (3 niveaux) : 3 unités
- Très grands (4 niveaux) : 1 unité
Total pour les triangles orientés vers le haut : 10 + 6 + 3 + 1 = 20.
Ajoutez maintenant les triangles inversés créés par l’intersection des traits : 7 unités.
Solution finale : 20 + 7 = 27.
Pour ne plus oublier : pensez « 20 qui montent, 7 qui descendent » et vous éviterez l’erreur classique.
La beauté mathématique de ce casse-tête

Vous aimez les approches plus théoriques ? Quand un triangle principal est divisé en n rangées grâce à des lignes parallèles à sa base (ici n = 4), cette formule magique donne la réponse :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce résultat correspond parfaitement à notre comptage minutieux. La force de cette équation ? Elle s’adapte à toutes les configurations possibles, même les plus complexes. Idéal pour valider son intuition… ou pour impressionner lors d’une soirée jeux entre amis !
Erreurs fréquentes (et comment les éviter)
- Compter « par étages » sans voir les formes qui traversent plusieurs niveaux : le coupable est souvent le triangle qui s’étend sur trois hauteurs.
- Oublier les triangles inversés : moins visibles, ils représentent pourtant 7 unités cruciales.
- Imaginer des lignes verticales supplémentaires : certaines variantes du défi en incluent effectivement, ce qui change le total (mais jamais vers 26). Vérifiez toujours le dessin exact avant de conclure.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour éviter les répétitions.
Pour aller plus loin dans le défi
- Changez le nombre de divisions : testez la formule avec n = 3 ou n = 5 et comparez avec un comptage visuel – excellent exercice pour affûter votre regard.
- Jouez contre la montre : donnez-vous 60 secondes pour atteindre 27. Le secret ? Repérez d’abord les triangles ascendants, puis ajoutez leurs versions descendantes.
- Transmettez l’astuce : expliquer une méthode, c’est la graver dans sa mémoire (et s’assurer de briller lors des prochains défis en groupe).
Car derrière une forme géométrique en apparence simple se cache souvent une leçon de logique imparable… et la satisfaction délicieuse de détenir la solution parfaite !









